Train Convolutional Neural Networks

Students are encouraged to use any Python framework and publicly available source code. Please credit and cite all references in your report. It is recommended to start work on this project as soon as possible to give yourself time.

• Problem Statement 1
• Problem Statement 2

Problem 1 (Train FC on MNIST)

This task consists of training a convolutional network to classify handwritten digits. Please write code to the following.

• Download the MNIST dataset that has gray scale images of hand written digits: Hugging Face website.

• Each image has 28x28 pixels. Hence each image in the dataset is a 2-dimensional matrix of size 28x28. In this Task 1.1 (but not in Task 1.2 which follows), flatten each input image into a 784 dimensional vector. (Note 28x28=784).

• Split the dataset into a training set (of 60000 images) and a test set (of 10000 images).

• Task 1.1 consists of training a neural network with one hidden layer consisting of 1000 neurons to classify digits. This is shown in Fig 1. By a single hidden layer of 1000 neurons, we mean that the 784 inputs are fully connected to 1000 neurons, which are in turn fully connected to 10 output identity neurons. There are ten output neurons since there are ten classes (0 to 9) into which each image is to be classified. A soft max follows the outputs of the identity neurons. Anything not connected to the inputs or outputs is called a hidden layer. The layer with 1000 neurons between and output is a hidden layer.

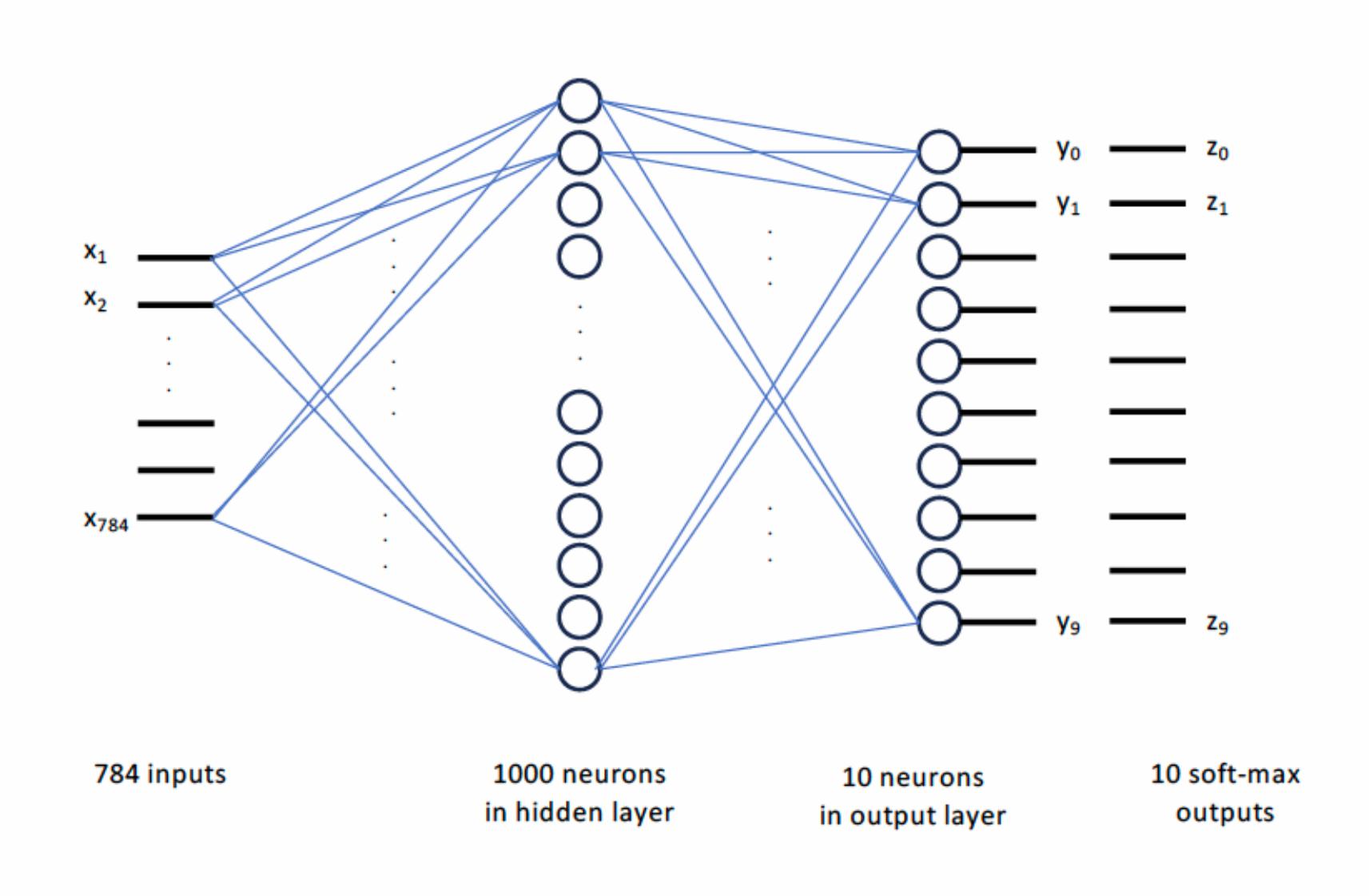
Figure 1: Neural network with one hidden layer of 1000 nodes. The 10 neurons in the output layer are Identity neurons; there is no nonlinearity. Each $y_i$ is just the weighted sum of the inputs to the Identity neuron. Note that $z_i = \frac{e^{y_i}}{e^{y_0} + e^{y_1} + \ldots + e^{y_9}}$ is the soft-max output.

• Apply the soft-max function to the output layer nodes, as shown, and utilize cross-entropy as the loss function. Experiment with different activation functions (RELU or Sigmoid) and gradient descent optimization methods.

• Plot training and test losses over 50 epochs to visualize the model’s learning performance.
• You may find the source code in Project 1 helpful for this task.

Task 1.2 Train A Convolutional Neural Network

• Take the same training and test data as in Task 1.1.
• For the 28x28 input, first apply a convolutional filter. Perform a single 2D convolutional operation on the input image with a 3x3 mask, unit stride, and no padding. The output is 26x26.

• You will need to feed this to the type of network in Task 1.1. There is one change though. Change the input size of neural network trained in Task 1.1 to 676 (=26x26). Feed the 676 outputs of the convolution layer to this network. and re-train the network, which is now called a convolutional neural network.

• Plot the training and test loss for 50 epochs.

• Did you observe an increase in the classification accuracy?

• Add another layer after the convolutional layer that performs a 3x3 max-pooling, and then connect its output to a fully-connected neural network, as in the previous bullet.

• Plot the training and test loss for 50 epochs.

• Comment on your observations. To answer this, you may want to plot the outputs of the convolution layer or convolution+max-pool layers as an image and compare it with the input image.

Task 1. 3 Permuted Images

• We will now permute all the pixel values in each image.
• We explain what we mean by a permutation. Consider an image of size 3x3. Suppose its pixels are \(\begin{bmatrix} x_{11} & x_{12} & x_{13}\\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix}.\) Then the following image is a permutation: \(\begin{bmatrix} x_{21} & x_{33} & x_{31}\\ x_{32} & x_{11} & x_{23} \\ x_{12} & x_{22} & x_{13} \\ \end{bmatrix}.\) In your case, since the images are 28x28, your permutation will also need to be 28x28.
• Choose a random permutation of the 28x28 image. Fig. 1 and 2 show one such permutation.

Figure 1: Example of original and permuted MNIST image

Figure 2: Example of original and permuted MNIST image

Problem 2:

2.1 Train RESNET-18 Architecture

• In this task, you will train the RESNET-18 architecture on the popular CIFAR-10 dataset, which consists of tiny colorful images categorized into 10 classes. You can access the dataset here.
• The code for downloading images and defining a neural network is available here.
• Create the RESNET-18 architecture as defined in Table 1 of the ResNet Paper. Implementing the plain RESNET-18 architecture is sufficient; there is no need to implement the residual architecture.
• Challenges you may encounter include size calculations of input and output at each layer. Resources such as the ConvNet size calculator, an overview of CNNs, and this Stack Overflow post can be helpful.
• Plot the training and testing accuracy for 50 epochs.

2.2: Train RESNET-18 Architecture on Permuted Dataset

• Randomly permute the images in the entire CIFAR-10 dataset. Make sure to apply the same permutation to all the images.
• Repeat Task 2.1 after the data has been permuted.

• Please make a report of your observations. Compare RESNET-18 performance on the permuted dataset. If you find any drop in performance, can you explain the reason?

• Permute all the images in the MNIST dataset with the same random permutation above. Permutation must be same for all images i.e., if your $x_{11}$ went to location $(18,5)$, then it should do so in all the images. Exercise great caution while doing this step, if you randomize each image differently, your network may not learn anything. You may find useful the code snippet provided below.

# freeze the seed, read more about the what it does to random sequence generation
np.random.seed(0)
num = random.randint(0, len(X_train))
plt.imshow(X_train[num], cmap='gray', interpolation='none')
plt.title("Class {}".format(y_train[num]))
test=X_train[num]
test.reshape(-1)
permuted_test=np.random.permutation(test)
permuted_test.reshape((28,28))
plt.subplot(2,2,2)
plt.xticks([])
plt.yticks([])
plt.imshow(permuted_test, cmap='gray', interpolation='none')
plt.title("Permuted Class {}".format(y_train[num]))
plt.tight_layout()

• Repeat Tasks 1.1 and 1.2 on the permuted dataset. Does the performance of Task 1.1 change after the permutation? Does the performance of Task 1.2 change after the permutation? Can you explain your answers?

References

1. Convnet Size Calculator. URL.

2. Deep Residual Learning for Image Recognition. arXiv.

3. MNIST Tutorials. PyTorch Lightning.

4. Overview of CNNs. CS231n.

5. PyTorch Tutorials. PyTorch.

6. Stack Overflow Post on CNN. Stack Overflow.